Física
En éste blog vamos a resolver algunos ejemplos y su teoría sobre varios temas que engloban a la física.
1.- Vector resultante (método analítico)
2.- Fricción de un cuerpo sobre un plano inclinado
3.- Momento (Torque)
4.- Tiro Parabólico
5.- 2da ley de Newton a un cuerpo
6.- Reflexión de espejos esféricos
ISAAC NEWTON (1643-1727)
Vector Resultante (Método Analítico)
Este método es el más fácil si se trata de la resolución clara y precisa del vector resultante.
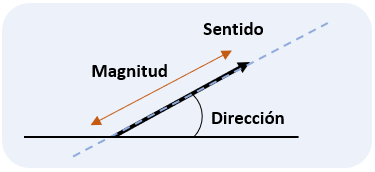
¿Qué es un vector y cuáles son sus características?
R= Es un término que deriva de un vocablo latino y que significa "que conduce". Un vector es un agente que transporta algo de un lugar a otro. Su significado, de todas formas, varía de acuerdo al contexto. Un vector debe tener magnitud, dirección y sentido, como se muestra en ésta imagen.
En un plano cartesiano se pueden encontrar tanto 1 como una infinidad de vectores, la sumatoria de dichos vectores forma un vector resultante, el vector resultante se obtendrá de dos vectores, los dos con magnitud y sentido sobre los dos ejes del plano cartesiano("x"&"y"), el signo de cada vector nos indicará hacia dónde va el vector tanto en "x" [arriba(vector positivo) ó abajo(vector negativo)] & "y" [izquierda(vector negativo) ó derecha(vector negativo)].
Y la sumatoria de todos los vectores en "x" se representa como FRx = Fuerza Resultante en X, y en "y" como FRy = Fuerza resultante en Y.
Luego sacaremos la magnitud del vector resultante, la raíz cuadrada de la sumatoria al cuadrado de la magnitud de FRx y FRy. Como se muestra en la siguiente imagen.
Finalmente, para obtener la dirección del vector resultante, se dividirá el arcotangente del valor absoluto de la división de (FRy/FRx), metiendo los datos a la calculadora sabremos a qué ángulo se encontrará nuestro vector sobre el eje de coordenadas. como se muestra en la sig. imagen
alfa es el ángulo con respecto a "x" del vector resultante
EJEMPLO
Tres embarcaciones ejercen fuerzas sobre un gancho de amarre como se muestra en la imagen. Halle la reultante de esas tres fuerzas.
1.- Debemos dibujar nuestro plano cartesiano con los tres vectores, anotar sus magnitudes y direcciones de cada vector respectivamente
F1=420N, a (60° - 0°)=60°
F2=150N, a 90°
F3=500N, a (180° - 40°)=140°
Nota:
No importa el orden de los vectores ni cómo los nombremos, siempre hay que aplicar nuestro diagrama de cuerpo libre, el ángulo siempre se calcula con respecto al eje x.
 2.-Trazamos los vectores dentro del plano
2.-Trazamos los vectores dentro del plano
3.- Calculamos las fuerzas tanto en x como en y, la sumatoria de fuerzas en los dos ejes se igualará a cero.
-Para el eje x, las fuerzas que se encuentren fuera del eje x(horizontal) se multiplicarán por coseno del ángulo con respecto al eje horizontal, y la fuerzas que se encuentren en el eje y (vertical) serán 0.
-Para el eje y las fuerzas que se encuentren fuera del eje y(vertical) se multiplicarán por seno del ángulo con respecto al eje horizontal, y la fuerzas que se encuentren en el eje x (horizontal) serán 0.
4.-En el eje x:
Sum F(x)=0
F1*cos(ϴ) + F2*cos(ϴ) + F3*cos(ϴ) = 0
Sustituimos valores:
Fx= 420N*cos(60°) + 150N*cos(90°) + 500N*cos(140°) = 0
Fx= 210N + (-383.02N) = -173.02N
En el eje y:
Sum F(y)=0
F1*sen(ϴ) + F2*sen(ϴ) + F3*sen(ϴ) = 0
Sustituimos valores:
Fy = 420N*sen(60°) + 150N*sen(90°) + 500N*sen(140°) = 0
Fy = 363.73N + 150N + 321.39N = 835.12 N
5.-Ya teniendo los valores de las sumatorias, tanto en x (Fx) como en y (Fy) sacaremos la magnitud.
Fuerza resultante(Fr)=Raíz[(-173.02N)^2 + (835.12N)^2]
Fr=852.85 N
6.-Finalmente obtendremos la dirección (ángulo) del vector:
Tan(ϴ)=(Fy/Fx)
ϴ = arctan(835.12/-173.02)
ϴ = -78.29°
Nota: el ángulo al ser negativo se le restarán 180°, ya que el vector se encuentra en el 2do cuadrante.
ϴ = 180° -78.29° = 101.7°
Fricción de un cuerpo sobre un plano inclinado
¿Qué es la fricción?
Fuerza de roce o de rozamiento es una fuerza existente entre dos superficies que se encuentran en contacto, y que se oponen al movimiento, en pocas palabras, fuerzas que se oponen al movimiento; pueden ser de dos tipos, estática (cuando se opone al incio de un desplazamiento) y dinámica (cuando se opone al movimiento relativo).
La fuerza estática Se trata de la fuerza necesaria vencer para iniciar el movimiento de un objeto. Es siempre menor o igual al coeficiente de rozamiento entre las dos superficies multiplicado por la fuerza normal.
Esta fricción estática suele ser mayor a la dinámica, lo cual explica por qué es más difícil empezar a empujar un mueble pesado sobre suelo rugoso, que seguir empujándolo una vez que ya está en movimiento.μs >= μk (Constantes de fricción "s" static y "k" kinetic; no tienen unidades).
Aquí podemos ver un ejemplo gráfico sobre el concepto de las dos frcciones:
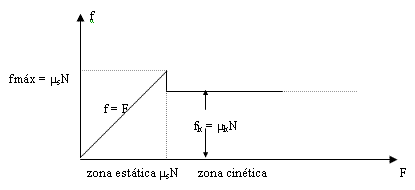
La fuerza máxima está dada por μk*N, dodne N es la normal.
¿Qué es la normal?
Es aquella superficie que ejerce una superficie como reacción a un cuerpo que ejerce fuerza sobre ella. Si la superficie es horizontal y no hay otra fuerza actuando que la modifique (por ejemplo la tensión de una cuerda hacia arriba), la fuerza normal es igual al peso pero en sentido contrario.
¿Qué es la normal?
Es aquella superficie que ejerce una superficie como reacción a un cuerpo que ejerce fuerza sobre ella. Si la superficie es horizontal y no hay otra fuerza actuando que la modifique (por ejemplo la tensión de una cuerda hacia arriba), la fuerza normal es igual al peso pero en sentido contrario.
EJEMPLO
¿Qué empuje P, dirigido hacia arriba del plano, hará que el bloque suba por dicho plano con rapidez constante?
1.-Anotar los datos que nos da el ejercicio:
-Peso del objeto (W) = 60N
-Constante de fricción dinámica (μk) = 0.3
-P = ?
- ϴ= 47°
Nota: El ángulo se calcula de acuerdo al triángulo rectángulo que se forma en el plano inclinado, la suma de los ángulos de un triángulo es 180°.
2.- Ya teniendo organizados los datos que nos da el problema, trazaremos nuestro plano cartesiano para una mejor visualización, anotaremos las fuerzas que actuan sobre nuestro cuerpo.
a) El peso (W)
b) La fuerza P
c) La fuerza de fricción cinética (Fk)
d) La normal (N)
El eje cartesiano es paralelo a nuestro plano inclinado.
3.- Ya trazados los vectores, haremos nuestra sumatoria de fuerzas en x & y igualando a 0.
Sum F(x)=0
P*cos(0°) + Fk*cos(180°) + W*cos(180° + 47°) = 0
P - Fk + 60N*cos(227°) = 0
ahora lo haremos con la Sum F(y)=0
N*sen(90°) + W*sen(227°) = 0
N = -(-43.88N)
N = 43.88N
4.- Teniendo la normal la vamos a sustituir en la fuerza de fricción
Fk = N*μk
Fk = 43.88N * 0.3
Fk = 13.16N
5.- Obtenido Fk la vamos a sustituir en la ecuación final de la Sum de F(x)
P - (13.16N) +(-40.91N) = 0
P = 13.16N + 40.91N
P = 54.07 N
Momento (Torque)
El momento de una fuerza o también llamado torque, es una magnitud vectorial que mide la capacidad que posee una fuerza para alterar la velocidad en giro de un cuerpo.
La ecuación del torque es:


1.- Debemos de ubicar nuestro punto (A) de giro en la figura, y las fuerzas que actúan sobre la barra.
2.- La fórmula para el momento del torque es:
Sum M(t) = t1 + t2 +t3+ ... + tn
Torque = F*d
En este caso, sería la distancia que se encuentra cada fuerza hacia el punto A.
Si la fuerza va hacia arriba con respecto al punto de giro (A) va a depender de qué lado se encuentre la fuerza con respecto al punto A; si está del lado izquierdo, girará como las manecillas del reloj, por lo tanto el momento de torque de esa fuerza será negativo.
Si la fuerza va hacia abajo con respecto al punto de giro (A), va a depender de qué lado se encuentre la fuerza con respecto al punto A; si está del lado izquiero, girará contrario a las manecillas del reloj, por lo tanto el momento del torque de esa fuerza será positivo, si la fuerza se encuentra del lado derecho del punto A, el momento del torque de dicha fuerza se moverá en sentido de las manecillas del reloj, por lo tanto será negativo el momento.
3.- Teniendo en cuenta todo lo que se dijo en el punto 2, vamos a calcular el momento de torque de las tres fuerzas:
T1 = (20N)*(-3m) = -60N*m
T2 = (15N)*(-2m) = -30N*m
T3 = (30N)*(4m+2m) = 180N*m /Recordemos que es la distancia de la fuerza hacia el punto de giro.
4.- Ya teniendo los tres momentos, los sumaremos:
M(t) = -60N*m -30N*m +180N*m
M(t) = 90N*m
El momento de una fuerza o también llamado torque, es una magnitud vectorial que mide la capacidad que posee una fuerza para alterar la velocidad en giro de un cuerpo.
La ecuación del torque es:

Donde:
T=Es el módulo del momento de una fuerza sobre un brazo de palanca, sus unidades son (N*m).
F=Es el módulo de la fuerza que se aplica sobre un cuerpo. Su unidad es el Newton.
r=Es el brazo de palanca, la distancia entre el giro y la recta sobre la que descansa la fuerza, su unidad es el metro.
Convenio de signos en el momento de una fuerza
El momento impulsa a los cuerpos a cambiar su velocidad de giro. Por esta razón suele incluirse un signo al módulo de fuerza, nos permitirá determinar hacia dónde va el impulso, si gira para un lado o para el otro.
1.-Cuando el impulso gira en el sentido de las agujas del reloj, el módulo del momento se acompaña de un signo negativo.
2.-Cuando el impulso gira en el sentido contrario a las agujas del reloj, el módulo del momento se considera positivo.
EJEMPLO
¿Cuál es el momento de torsión resultante respecto al punto A? No tome en cuenta el peso de la barra.

1.- Debemos de ubicar nuestro punto (A) de giro en la figura, y las fuerzas que actúan sobre la barra.
2.- La fórmula para el momento del torque es:
Sum M(t) = t1 + t2 +t3+ ... + tn
Torque = F*d
En este caso, sería la distancia que se encuentra cada fuerza hacia el punto A.
Si la fuerza va hacia arriba con respecto al punto de giro (A) va a depender de qué lado se encuentre la fuerza con respecto al punto A; si está del lado izquierdo, girará como las manecillas del reloj, por lo tanto el momento de torque de esa fuerza será negativo.
Si la fuerza va hacia abajo con respecto al punto de giro (A), va a depender de qué lado se encuentre la fuerza con respecto al punto A; si está del lado izquiero, girará contrario a las manecillas del reloj, por lo tanto el momento del torque de esa fuerza será positivo, si la fuerza se encuentra del lado derecho del punto A, el momento del torque de dicha fuerza se moverá en sentido de las manecillas del reloj, por lo tanto será negativo el momento.
3.- Teniendo en cuenta todo lo que se dijo en el punto 2, vamos a calcular el momento de torque de las tres fuerzas:
T1 = (20N)*(-3m) = -60N*m
T2 = (15N)*(-2m) = -30N*m
T3 = (30N)*(4m+2m) = 180N*m /Recordemos que es la distancia de la fuerza hacia el punto de giro.
4.- Ya teniendo los tres momentos, los sumaremos:
M(t) = -60N*m -30N*m +180N*m
M(t) = 90N*m
Tiro Parabólico
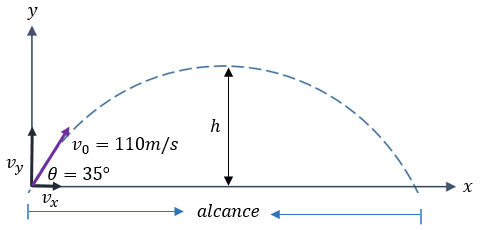

Es un movimmiento que resulta de la unión de dos movimientos: El movimiento rectilíneo uniforme (componentes en horizontal), y el movimiento vertical (componente vertical) que se efectúa por la gravedad y el resultado es una parábola.
Un MRU horizontal de velocidad Vx siempre será constante, por lo tanto la aceleración es 0, a(x)=0.
Las ecuaciones paramétricas para X & Y:
x=Vo*cos(ϴ)*t
y=Yo+Vo*sen(ϴ)*t-(g*(t^2))/2
donde:
x=posición inicial
Vo=Velocidad inicial
ϴ=El ángulo con el que se le lanza al objeto
t=tiempo
y=altura final
Yo=altura inicial
g=gravedad

Aquí hay tres fórmulas fundamentales en un tiro parabólico:

Ymax=Altura máxima.
Tvuelo=tiempo del objeto en el aire.
Xmax=alcance.
EJEMPLO
En la imagen, una pelota de golf sale del punto de partida, al ser golpeada, con una velocidad de 40m/s a 65°. Si cae sobre un green ubicado a 10m más arriba que el punto de partida, ¿cuál fue el tiempo que permaneción en el aire y cuál fue la distancia horizontal recorrida respecto al palo?
1.- Anotamos los datos que nos da el problema y los datos que debemos encontrar
Vo=40m/s
ϴ=65°
y=10m
t=?
x=?
2.-Aplicaremos nuestras fórmulas previamente anotadas, tanto para x(alcance) como para y(altura final):
x = Vo*cos(ϴ)*t
x = (40m/s)*cos(65°)*t
Para saber el alcance final, tenemos las dos incógnitas que nos pide el problema, entonces vamos a seguir con la fórmula para y(altura final).
y=Yo+Vo*sen(ϴ)*t-(g*(t^2))/2
Nota:nuestra Yo es la altura inicial con la que es lanzada la pelota de golf, como fue lanzada del piso, su altura será 0
10m = 0m + 40m/s*sen(65°)*t - 4.905t^2
3.-Resolvemos nuestra ecuación en y, pasando la altura final del otro lado de la ecuación:
-4.905t^2 + 36.25m/s -10m = 0
Si nos fijamos, es una ecuación cuadrática, por lo tanto va a haber dos resultados en la variable a despejar, que es nuestro tiempo, resolveremos por el método general;
t = [ - 36.25 +- Raíz((36.25)^2 - 4*(-4.905)*(-10)) ] / (2*-4.905)
t1 =0.28s //éste resultado es físicamente imposible, la pelota no puede recorrer una distancia larga en tan poco tiempo, ni medio segundo.
t2 = 7.11s //Tomaremos éste valor como el bueno.
4.-Teniendo el tiempo que recorrió la pelota en el aire, ahora calcularemos el alcance en esos 7.11s:
x = (40m/s)*cos(65°)*(7.11s)
x=120.2m
x = (40m/s)*cos(65°)*t
Para saber el alcance final, tenemos las dos incógnitas que nos pide el problema, entonces vamos a seguir con la fórmula para y(altura final).
y=Yo+Vo*sen(ϴ)*t-(g*(t^2))/2
Nota:nuestra Yo es la altura inicial con la que es lanzada la pelota de golf, como fue lanzada del piso, su altura será 0
10m = 0m + 40m/s*sen(65°)*t - 4.905t^2
3.-Resolvemos nuestra ecuación en y, pasando la altura final del otro lado de la ecuación:
-4.905t^2 + 36.25m/s -10m = 0
Si nos fijamos, es una ecuación cuadrática, por lo tanto va a haber dos resultados en la variable a despejar, que es nuestro tiempo, resolveremos por el método general;
t = [ - 36.25 +- Raíz((36.25)^2 - 4*(-4.905)*(-10)) ] / (2*-4.905)
t1 =0.28s //éste resultado es físicamente imposible, la pelota no puede recorrer una distancia larga en tan poco tiempo, ni medio segundo.
t2 = 7.11s //Tomaremos éste valor como el bueno.
4.-Teniendo el tiempo que recorrió la pelota en el aire, ahora calcularemos el alcance en esos 7.11s:
x = (40m/s)*cos(65°)*(7.11s)
x=120.2m
2da ley de Newton a un cuerpo
La segunda ley de Newton establece que las aceleraciones que experimenta un cuerpo son proporcionales a las fuerzas que recibe. Una fuerza es un empujón o jalón que se ejerce sobre un objeto, pueden ser varias fuerzas que actúen sobre un cuerpo, entonces será la sumatoria de todas esas fuerzas igual a la masa de dicho cuerpo por la aceleración con el que se mueve.
Su fórmula es:
F= m*a
donde:
F=Fuerza con la que se acelera el objeto.
m=masa.
a=aceleración.
EJEMPLO
En la imagen, una masa desconocida desciende deslizándose por el palno inclinado a 30°. ¿Cuál es la aceleración si no existe fricción alguna?
1.- Vamos a trazar nuestras fuerzas que actúan sobre nuestro objeto, como el objeto está deslizándolo hacia abajo del plano inclinado sin ninguna fuerza externa, entonces tendremos el peso del objeto y la normal:

El ángulo es de 30° con respecto al eje y, al ser un triángulo semejante, notaremos que es el mismo ángulo que el del plano inclinado.
2.- Ya trazados nuestros vectores, haremos la sumatoria en x igualando la a masa por la aceleración
Sum F(x) = m*a
Wsen(30°) = m*a
m*g*sen(30°) = m*a
g*sen(30°) = a
(9.81m/s^2)*(0.5) = a
a = 4.905 m/s^2
1.- Vamos a trazar nuestras fuerzas que actúan sobre nuestro objeto, como el objeto está deslizándolo hacia abajo del plano inclinado sin ninguna fuerza externa, entonces tendremos el peso del objeto y la normal:

El ángulo es de 30° con respecto al eje y, al ser un triángulo semejante, notaremos que es el mismo ángulo que el del plano inclinado.
2.- Ya trazados nuestros vectores, haremos la sumatoria en x igualando la a masa por la aceleración
Sum F(x) = m*a
Wsen(30°) = m*a
m*g*sen(30°) = m*a
g*sen(30°) = a
(9.81m/s^2)*(0.5) = a
a = 4.905 m/s^2
Óptica
La reflexión de la luz es el cambio en la dirección que expeimenta un rayo cuando incide sobre una superficie opaca. la luz se propaga en línea recta a una velocidad de 3x10^8 m/s. Si cambia el medio, la rapidez también cambiará y la luz viajará en línea recta a lo largo de una nueva trayectoria. La desviación de un rayo de luz cuando pasa oblicuamente de un medio a otro se conoce como refracción.
Los mismo métodos geométricos aplicados a la reflexión de luz de un espejo plano se puede ocupar en un espejo curvo, puede haber dos tipos de espejos, cóncavos y convexos.
Clasificación de las imágenes según su naturaleza:
*Reales: Se forman cuando los rayos reflejados después de interactuar con un espejo o lente, se intersectan en un punto. La imagen debe proyectarse sobre un plano o pantalla para ser visible.
*Virtuales: Se forman cuando los rayos después de interactuar con un espejo o lente. divergen y son sus proyecciones las que se unen en un punto. Estas imágenes so se pueden proyectar en un plano, pero son visibles para el observador.
Con respecto a la posición, las imágenes pueden ser:
*Derechas: Si están orientadas igual que el objeto.
*Invertidas: Si están en la posición contraria al objeto.
Según su tamaño las imágenes se denominan:
Aumentadas: si son más grandes que el objeto.
Disminuidas: si son más pequeñas en relación al objeto.
La ecuación para encontrar las distancias será:
1/f = 1/p + 1/q
Distancia del foco al espejo
f = C/2
Amplificación de la imagen
M = -q/p
M = y´ / y
donde:
f = distancia focal
p = distancia del objeto
q = distancia de la imagen
C = radio de curvatura
y = tamaño del objeto
y´ = tamaño de la imagen
M = amplificación
La ecuación para encontrar las distancias será:
1/f = 1/p + 1/q
Distancia del foco al espejo
f = C/2
Amplificación de la imagen
M = -q/p
M = y´ / y
donde:
f = distancia focal
p = distancia del objeto
q = distancia de la imagen
C = radio de curvatura
y = tamaño del objeto
y´ = tamaño de la imagen
M = amplificación
Aquí podemos ver un ejemplo de un espejo cóncavo y un espejo convexo
Donde:
O=Radio de curvatura del espejo
F=Punto focal
Aquí podemos ver varios ejemplos de espejos cóncavos:
Aquí podemos ver varios ejemplos de espejos cóncavos:
donde:
y = objeto
y´ = imagen
C = radio de curvatura
O = Eje focal
F = foco
EJEMPLO
Un lápiz de 8cm de largo se coloca a 10cm de un espejo divergente que tiene 30cm de radio. Determine la naturaleza, el tamaño y la ubicación de la imegen que se forma. Haga el diagrama de rayos.
1.- Anotemos los datos que nos da el problema y las incógnitas
y = 8cm
p = 10cm
C = 30cm
¿Virtual o Real?
y´ = ?
q = ?
2.- Escribiremos las fórmulas que necesitaremos:
Ecuación para encontrar el foco de un espejo:
f = C/2
f= 30cm/2
f= -15cm
La distancia del foco será negativa, porque es un espejo divergente
Ecuación de la distancia focal:
1/f = 1/p + 1/q
vamos a tener que despejar "q" aplicando las operaciones necesarias obtendremos q:
q = (p*f)/(p-f)
sustituimos valores
q = (10cm * -15cm)/(10cm - (-15cm))
q = -6cm
3.- Obtendremos la amplificación de nuestra imagen ahora que sabemos su distancia al espejo divergente:
Amplificación = -q / p = y´/ y = M
M = - (-6cm) / (10cm) = 0.6
y´ / y = 0.6
y´ = (0.6)*8cm
y´= 4.8cm
4.- Como conclusión final, diremos las caracteríticas de nuestra imagen:
"Es una imagen virtual que se encuentra a 6 cm del espejo, no está invertida y se encuentra disminuida con respecto al objeto, 4.8 cm mide."
5.- Finalmente trazaremos el diagrama de rayos.











Comentarios
Publicar un comentario